


Each entry a kl of Transition matrix A denotes the probability of transition from.
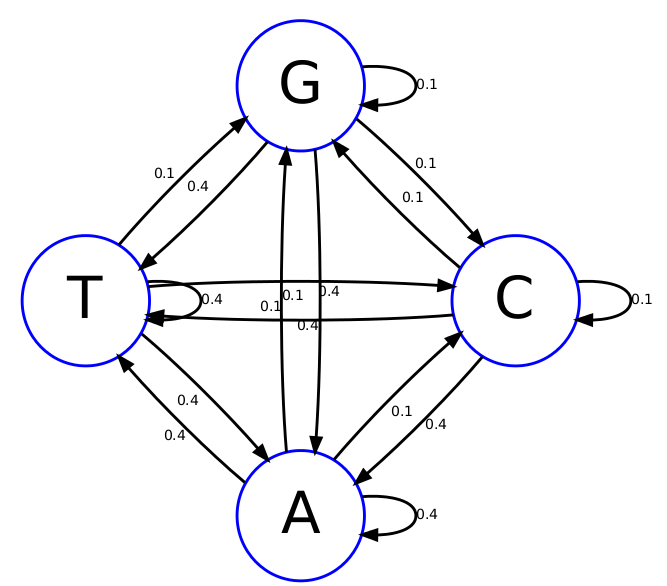
Vector represents the hidden path, which is the sequence of hidden states. Vector x represents sequence of observations. The usefulness of this contribution to the Lanchester theory of combat is discussed. For example, the Markov chain (MC) model was employed to forecast the urban LULC changes in the Bhagirathi-Hugli River, India 40. To take a closer look at Hidden Markov Model, let’s first define the key parameters in Figure 7.3. The multivariate Markov chain model is a model that is used. It is also shown that the reciprocal of an element of the mean first passage time matrix of the Markov chain model of the generalized combat process can be defined as the Lanchester attrition coefficient for a square law combat process. The data that belong to the system being analyzed in the Markov chains stem from a single source. Some statistical techniques for estimating the one-step transition probabilities are given, and methods for modeling deterministic and stochastic action times, i.e., the amount of time that the process remains in a given state are presented. The mean and variance of the first passage times to certain states and the limiting distribution of the amount of time that the process remains in a given state are suggested as being useful measures of the effectiveness of a weapons system. This section describes how the model is reduced in size and adapted for situations where the Markov chain is non-homogenous with respect to time. Abstract: A generalized combat process is structured as a regular finite Markov chain with states reflecting the control, maneuver, target acquisition, and target destruction actions of a weapons system. model to be a Markov chain model, and its use in modeling system evolution.


 0 kommentar(er)
0 kommentar(er)
